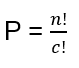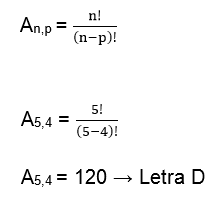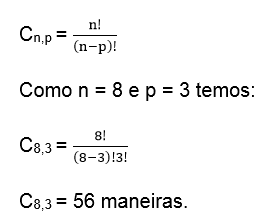PRINCÍPIO FUNDAMENTAL DA CONTAGEM.
No PRINCÍPIO FUNDAMENTAL DA CONTAGEM, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.
Exemplo:
Cleópatra irá participar da promoção de uma loja de roupas que está dando um vale compras no valor de R$ 1.000,00 reais.
Ganhará o desafio o primeiro participante que conseguir fazer o maior número de combinações com o kit de roupa cedido pela loja.
No kit, temos:
Seis camisetas, quatro saias e dois pares de sapato do tipo salto alto.
De quantas maneiras distintas Cleópatra poderá combinar todo o vestuário que esta no quite de roupa?
Solução:
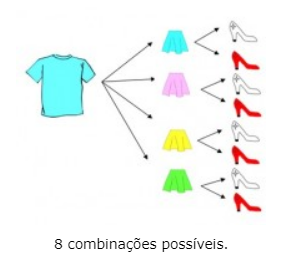
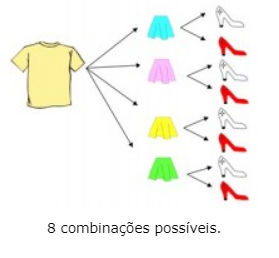
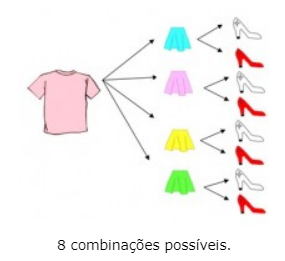
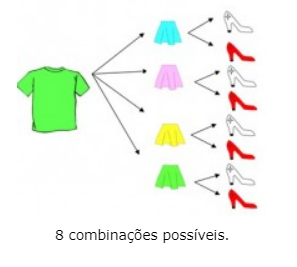
Peças que compõem o kit de roupas:
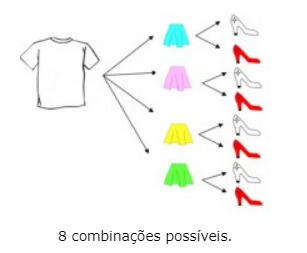
Vamos fazer um esquema para entender melhor e descobrir a quantidade de combinações possíveis.
Ao realizar a contagem iremos constatar a quantidade referente a 48 combinações possíveis.
A outra forma que temos para resolver este problema é utilizando o PRINCÍPIO FUNDAMENTAL DA CONTAGEM.
Total de Camisetas x Total de Saias x Total Sapatos = Total de Combinações Possíveis
6 x 4 x 2 = 48
Tipos de Combinatória
O PRINCÍPIO FUNDAMENTAL DA CONTAGEM pode ser usado em grande parte dos problemas relacionados com contagem.
Entretanto, em algumas situações seu uso torna a resolução muito trabalhosa.
Desta maneira, usamos algumas técnicas para resolver problemas com determinadas características.
Basicamente há três tipos de agrupamentos: arranjos, combinações e permutações.
Antes de conhecermos melhor esses procedimentos de cálculo, precisamos definir uma ferramenta muito utilizada em problemas de contagem, que é o FATORIAL.
O FATORIAL de um número natural, é definido como o produto deste número por TODOS os seus ANTECESSORES.
Utilizamos o símbolo “!” (ponto de exclamação) para indicar o FATORIAL de um número.
Define-se ainda que o fatorial de zero é igual a 1.
Exemplo
O! = 1
1! = 1
3! = 3 x 2 x 1 = 6
7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5.040
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 3.628.800
Note que o valor do fatorial cresce rapidamente, conforme cresce o número.
Então, frequentemente usamos simplificações para efetuar os cálculos de análise combinatória.
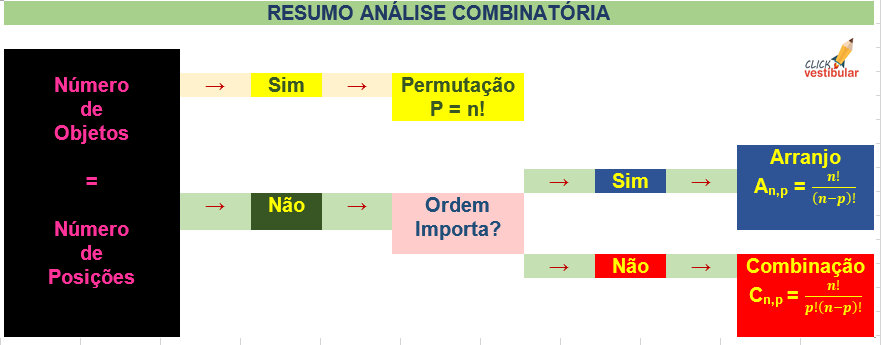
Como saber quando utilizar Permutação, Arranjo ou Combinação?
Para diferenciar se é Arranjo, Permutação ou Combinação vocês têm que fazer a seguinte pergunta:
O NÚMERO DE OBJETOS é IGUAL ao NÚMERO DE POSIÇÕES?
Se a resposta for SIM, então você utiliza PERMUTAÇÃO.
Começaremos com exemplos bem simples e gradativamente vamos aumentando a dificuldade, bem devagar, sem pressa, de boa.
Exemplo 01:
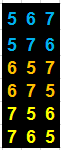
Temos os números 5, 6 e 7. De quantas maneiras distintas pode ter ocorrido essa sequência de resultados?
Solução
Identificação das partes envolvidas:
Número de Objetos: 5,6,7 → 3 objetos.
Número de Posições que os objetos possam assumir: _, _, _→ 3 posições.
Logo:
3 OBJETOS = 3 POSIÇÕES → PERMUTAÇÃO
Percebam que os 3 objetos (5,6,7) podem assumir qualquer posição.
Temos:
5, 6, 7
Ou
6, 7, 5
Ou
7, 5, 6 e assim por diante.
Então, se NÚMERO DE OBJETOS = NÚMERO DE POSIÇÕES que estes objetos possam assumir, temos:
Ou seja, teremos 6 maneiras distintas de dispor estes 3 objetos.
Percebam que neste exemplo, utilizamos apenas 3 objetos, e olhem o trabalho que deu.
Imagine um caso onde temos o número de objetos muito grande.
Por isso, que existem as fórmulas.
E a fórmula da Permutação é:
P = n!
Agora, utilizando a fórmula, temos:
P = n! → onde, “n” representa o número de objetos, temos:
P = 3! → substitui o 3 (objetos) pelo “n”
P = 3 x 2 x 1
P = 6 maneiras distintas (chegamos ao mesmo resultado sem muito esforço).
Exemplo 02:
Quantos anagramas podemos formar com a palavra AMOR?
Portanto, temos:
Identificação das partes envolvidas:
Número de Objetos: A, M, O, R → 4 objetos.
Número de Posições: _, _, _, _ → 4 posições.
Percebam que os 4 objetos (A, M, O, R) podem assumir qualquer posição.
Se NÚMERO DE OBJETOS = NÚMERO DE POSIÇÕES, temos:
Ou seja, teremos 24 maneiras distintas de dispor estes 4 objetos.
Agora, utilizando a fórmula da Permutação, temos:
P = n!
P = 4!
P = 4 x 3 x 2 x 1
P = 24 maneiras distintas (chegamos ao mesmo resultado sem muito esforço).
Nos exemplos seguintes, vamos ver o que seria uma Permutação com Repetição.
Permutação de elementos repetidos deve seguir uma forma diferente da permutação, pois elementos repetidos permutam entre si.
Vejam os Modelos abaixo:
Modelo 01:
Quantos anagramas distintos podemos formar com a palavra OVO?
Solução
OVO;
OOV;
VOO.
Apenas 3.
Mas como, se com os 3 objetos (5, 6, 7) formamos 6 anagramas, e com os 3 objetos (O, V, O) formamos apenas 3 anagramas?
É porque na palavra OVO temos objetos repetidos.
Veja bem:
Com o anagrama VOO se fixamos o V e invertemos apenas os “O” teremos novamente o anagrama VOO que é o mesmo anagrama, portanto não conta.
Modelo 02:
Quantos anagramas distintos podemos formar com a palavra MATEMÁTICA?
Sem levar em consideração os objetos repetidos, a permutação ficaria assim:
Identificação das partes envolvidas:
Número de Objetos: M, A, T, E, M, Á, T, I, C, A → 10 objetos.
Número de Posições: _, _, _, _, _, _, _, _, _, _ → 10 posições.
Usamos a fórmula, temos:
P = n!
P10 = 10!
P10 = 3.628.800
Agora, a palavra MATEMÁTICA possui elementos que repetem, acompanhe:
a! = 3! → equivale ao objeto “A” que repete 3 vezes na palavra MATEMÁTICA.
t! = 2! → equivale ao objeto “T” que repete 2 vezes na palavra MATEMÁTICA.
m! = 2! → equivale ao objeto “M” que repete 2 vezes na palavra MATEMÁTICA.
Substituindo na fórmula, temos:
P = a! x t! x m! → permutação apenas dos objetos que repetem
P = 3! x 2! x 1!
P = (3 x 2 x 1) x (2 x 1) x (2 x 1)
P = 6 x 2 x 2
P = 24 → 24 combinações apenas dos objetos que se repetem
Logo, a permutação da palavra MATEMÁTICA será:
Portanto, com a palavra MATEMÁTICA podemos montar 151.200 anagramas.
Exemplo 03:
Questão de concurso:
(LEGALLE – 2019) Com as letras da palavra CODECA o número de anagramas possíveis de serem formulados è:
a) ( ) 120.
b) ( ) 360.
c) ( ) 2.160.
d) ( ) 4.320.
Olha aí!!! Galera, atentem ali, para a palavra ANAGRAMA, se tem ANAGRAMA, tem PERMUTAÇÃO.
Veremos então:
Identificação das partes envolvidas:
Número de Objetos: C, O, D, E, C, A → 6 objetos.
Agora, temos que cuidar, porque a letra “C”, repete quantas vezes?
A letra “C” repete 2 vêzes, então, basta fazer:
Para os termos que repetem e que são colocados no denominador, utilizamos qualquer letra (neste caso, usei o “c” para representar o 2), exceto o “n”, pois o mesmo já representa o número total de objetos.
Exemplo 4
Determine o número de anagramas que podem ser formados com as letras do nome ALEMANHA.
Identificação das partes envolvidas:
Número de Objetos: A, L, E, M, A, N, H, A → 8 objetos.
Agora, temos que cuidar, porque a letra “A”, repete quantas vezes?
A letra “A” repete 3 vêzes, então, basta fazer:
Exemplo 5
Utilizando o nome COPACABANA, calcule o número de anagramas formados desconsiderando aqueles em que ocorrem repetições consecutivas de letras.
Identificação das partes envolvidas:
Número de Objetos: C, O, P, A, C, A, B, A, N, A → 10 objetos.
Agora, temos que cuidar, porque as letras “A” e “C”, repetem quantas vezes?
A letra “A” repete 4 vêzes,
A letra “C” repete 2 vêzes, então, basta fazer:
Exemplo 6
Na palavra NORTE, quantos anagramas podem ser formados? Quantos começam com vogal?
Identificação das partes envolvidas:
Número de Objetos: N, O, R, T, E → 5 objetos.
Portanto:
P = n!
P = 5!
P = 5 x 4 x 3 x 2 x 1
P = 120.
Para sabermos quantos começam com vogal, sabemos que, fixado que a primeira letra é uma vogal, restam apenas quatro posições a serem permutadas.
Então, temos:
P = n!
P = 4!
P = 4 x 3 x 2 x 1
P = 24.
Como temos duas vogais, basta multiplicar 2 x 24 = 48.
Assim, dos 120 anagramas que podem ser formados, apenas 48 começam com vogais.
Utilizando Arranjo ou Combinação
Agora fazendo a pergunta novamente:
O NÚMERO DE OBJETOS é IGUAL ao NÚMERO DE POSIÇÕES?
Se a resposta for NÃO, então você faz a segunda pergunta:
A ORDEM IMPORTA?
Se a resposta for SIM, você utiliza ARRANJO.
Se a resposta for NÃO, você utiliza COMBINAÇÃO.
Veja os exemplos:
Exemplo 07:
Em uma urna de sorteio de prêmios existem dez bolas enumeradas de 0 a 9. Determine o número de possibilidades existentes num sorteio cujo prêmio é formado por uma sequência de 6 algarismos.
Fazendo a pergunta:
O NÚMERO DE OBJETOS é IGUAL ao NÚMERO DE POSIÇÕES?
NÃO, porque temos 10 objetos e 6 posições.
A segunda pergunta:
A ORDEM IMPORTA?
SIM, note que a sequência 1,3,5,6,7,9 é diferente da sequência 9,7,6,5,3,1.
Logo vamos utilizar a fórmula do ARRANJO, temos:
Onde, “n” é o número de objetos, ou seja, n = 10.
E “p” o número de posições, ou seja, p = 6.
Então temos:
Exemplo 08:
(Liquigás – CESGRANRIO 2012). Em uma pequena sala de projeção, há cinco cadeiras dispostas em linha, lado a lado, e numeradas de 1 a 5.
Quatro pessoas vão ocupar quatro dessas cadeiras. As possíveis ocupações das cadeiras distinguem-se não só pela cadeira vazia, mas, também, pela disposição das pessoas nas cadeiras ocupadas.
De quantos modos as cadeiras podem ser ocupadas pelas quatro pessoas?
a) 5
b) 20
c) 24
d) 120
e) 1.024
Fazendo a pergunta:
O NÚMERO DE OBJETOS é IGUAL ao NÚMERO DE POSIÇÕES?
NÃO, porque temos 5 objetos e 4 posições.
A segunda pergunta:
A ORDEM IMPORTA?
SIM, note que explorando a ideia de que 4 cadeiras em 5 serão escolhidas, e que a ordem em cada uma delas é importante, temos:
Exemplo 9
Um pesquisador científico precisa escolher três cobaias, num grupo de oito cobaias.
Determine o número de maneiras que ele pode realizar a escolha.
Fazendo a pergunta:
O NÚMERO DE OBJETOS é IGUAL ao NÚMERO DE POSIÇÕES?
NÃO, porque temos 8 cobaias e vamos escolher 3.
A segunda pergunta:
A ORDEM IMPORTA?
NÃO, ordem não importa, note que se numerarmos as cobaias de 1 a 8. E escolhermos a cobaia 2, 4, e 5 é a mesma coisa que escolher a cobaia 4,5 e 2.
Logo é uma COMBINAÇÃO onde o “n” que é o número de objetos que é 8 e “p” que é o número de elementos a serem escolhido que é 3, temos:
Exemplo 10
Um fabricante de sorvetes possui a disposição 7 variedades de frutas: uva, abacaxi, limão, coco, abacate, banana e cereja, e pretende misturá-las duas a duas na fabricação de sorvetes.
Quantos serão os tipos de sorvete disponíveis?
Fazendo a pergunta:
O NÚMERO DE OBJETOS é IGUAL ao NÚMERO DE POSIÇÕES?
NÃO, porque temos 7 objetos e vamos escolher 2.
A segunda pergunta:
A ORDEM IMPORTA?
NÃO, Os sorvetes de UVA COM ABACAXI e de ABACAXI COM UVA, na verdade tratam-se de um MESMO TIPO DE SORVETE, portanto é um caso de COMBINAÇÃO, logo temos:
Agora o resumo para você não se confundir mais: